Giới hạn của hàng số là một điểm kim chỉ nan phổ biến thường có trong đề thi thpt Quốc Gia. Vì vậy việc nắm rõ khái niệm cũng như cách giải bài bác tập để giúp đỡ ích hơn cho các em trong những khi thi. Hãy thuộc Marathon Education tò mò kỹ rộng trong bài viết sau đây!
Lý thuyết số lượng giới hạn của hàng số
Dãy số có số lượng giới hạn 0
Định nghĩa 1:
Dãy số (un ) có số lượng giới hạn bằng 0 lúc n dần dần tới dương vô cực, giả dụ giá trị hoàn hảo và tuyệt vời nhất của n gồm thể nhỏ dại hơn một số dương nhỏ tùy ý, đông đảo số hạng của dãy số và tính từ lúc số hạng ngẫu nhiên nào kia trở đi.
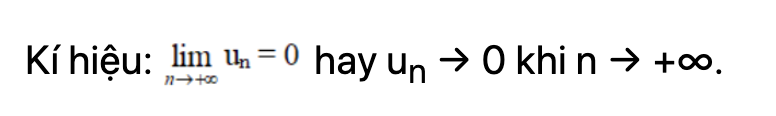
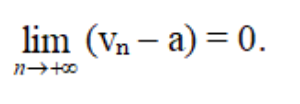

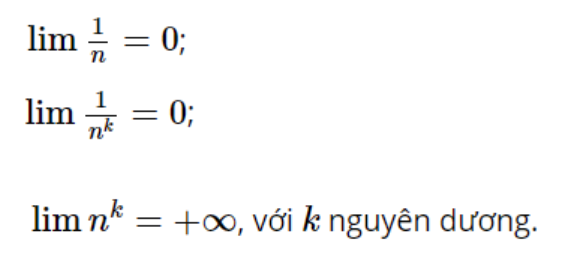
Dãy số có số lượng giới hạn vô cực
Dãy số có số lượng giới hạn +∞
Dãy số có số lượng giới hạn (un ) nếu với mọi số dương bất kỳ, đa số số hạng của hàng số, kể từ một số hạng nào kia trở đi phần nhiều sẽ lớn hơn số dương đó.
Ký hiệu: lim un = + ∞.
Dãy số có số lượng giới hạn – ∞
Dãy số có giới hạn (un ) nếu với tất cả số âm bất kỳ cho trước, hầu như số hạng của dãy số, kể từ một số hạn nào đó trở đi phần lớn sẽ nhỏ dại hơn số âm đó.
Ký hiệu: lim un = – ∞.
Bạn đang xem: Công thức tính giới hạn
Các phép tắc tìm số lượng giới hạn vô cực
Quy tắc nhân
Dãy số có giới hạn hữu hạn
Định nghĩa:



Các định lý:
Nếu lim un = a với lim vn = b, thì:lim (un + vn) = a + b.lim (un – vn) = a – b.lim (un.vn) = ab.

Các dạng bài bác tập về số lượng giới hạn dãy số tất cả lời giải
Dạng 1: Tìm giới hạn của hàng số
Phương pháp giải: thực hiện định nghĩa, phối hợp tính hóa học và hầu như định lý về giới hạn của một dãy số
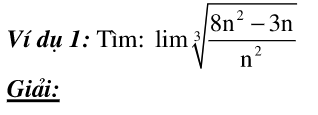

Dạng 3: minh chứng lim un tồn tại
Phương pháp giải: sử dụng định lý
Dãy số (un ) tăng với bị chặn trên thì tất cả giới hạnDãy số (vn ) sút và bị ngăn dưới thì có giới hạn
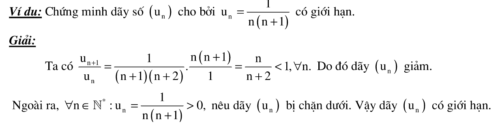
Dạng 4: Tính tổng của cấp cho số nhân lùi vô hạn
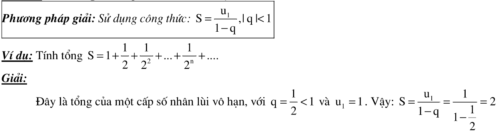
Dạng 5: Tìm giới hạn vô cực
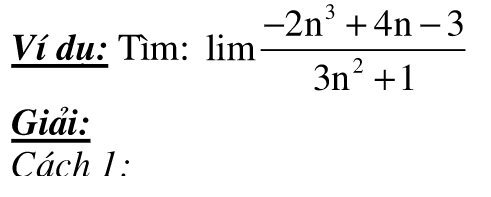

Tham khảo ngay các khoá học online của Marathon Education
Như vậy, các em vẫn được tìm hiểu về định hướng giới hạn của hàng số cũng giống như cách giải bài xích tập 1-1 giản, chi tiết. Hy vọng với những kỹ năng được team Marathon truyền tải, những em hoàn toàn có thể dễ dàng ôn luyện và giải bài tác dụng hơn.
Hãy contact ngay với Marathon để được support nếu các em có nhu cầu học online cải thiện kiến thức nhé! Marathon Education chúc những em ăn điểm cao trong số bài khám nghiệm và kỳ thi sắp đến tới!
Marathon – gốc rễ lớp học trực tuyến đường hàng đầu, cung cấp giải pháp giáo dục toàn diện ngoài trường học đến tất cả học sinh trên toàn nước với chất lượng tốt nhất!Tìm gọi thêm về Marathon tại:
Địa chỉ 1: Tầng 9, Tòa bên Lim Tower 3, 29A Nguyễn Đình Chiểu, Phường Đa Kao, Quận 1, TP. Hồ Chí Minh.
Địa chỉ 2: tầng trệt – 3 ,Tòa đơn vị Yoko Building, 677/6 Điện Biên Phủ, Phường 25, Quận Bình Thạnh, TP. Hồ Chí Minh
Nội Dung
Công thức tính lim số lượng giới hạn của hàm sốGiới hạn của hàm số
Tìm giới hạn vô cùng của một hàng số
Công thức tính lim giới hạn của hàm số
Khi giải các bài toán về số lượng giới hạn của hàm số, cách làm tính lim số lượng giới hạn của hàm số là trong số những kiến thức quan tiền trọng. Nó giúp họ xác định số lượng giới hạn của hàm số một cách chính xác và hiệu quả. Dưới đó là công thức tính lim giới hạn của hàm số:
Công thức 1: Dùng số lượng giới hạn của một hàm số để tính số lượng giới hạn của hàm số khác
Giả sử họ đã biết giới hạn của hàm số f(x) khi x tiến đến a. Giả dụ hàm số g(x) rất có thể viết dưới dạng g(x) = (f(x) – b)/(x – a) với b là một số hữu hạn, thì số lượng giới hạn của hàm số g(x) lúc x tiến mang lại a cũng đó là giá trị của f"(a), tức là:
limx→a g(x) = f"(a) = limx→a
Ví dụ: đến hàm số f(x) = x2 + 3x – 2 và hàm số g(x) = (x2 – 1)/(x – 1). Ta ý muốn tính giới hạn của hàm số g(x) khi x tiến đến 1. Nhận ra rằng g(x) rất có thể viết dưới dạng g(x) = f(x) + 2/(x – 1), bởi đó:
limx→1 g(x) = limx→1
Công thức 2: Dùng những quy tắc tính số lượng giới hạn để tính giới hạn của hàm số
Các phép tắc tính giới hạn của các hàm số cơ bản như hàm mũ, lượng chất giác, hàm logarith, hàm mũ trùng phương, hàm căn bậc hai… cũng rất có thể được áp dụng để tính giới hạn của một hàm số tinh vi hơn. Để sử dụng những quy tắc này, họ cần so với hàm số kia thành những thành phần cơ bản, tiếp nối áp dụng những quy tắc khớp ứng để tính giới hạn.
Công thức 3: Sử dụng giới hạn bất định
Trong một vài trường hợp, ta có thể sử dụng số lượng giới hạn bất định nhằm tính giới hạn của hàm số. Nếu lúc tính giới hạn, ta nhận thấy một biểu thức không xác định dạng 0/0 hoặc ∞/∞, ta rất có thể áp dụng những kỹ thuật rút gọn, phân chia tử cùng mẫu để mang biểu thức về dạng rất có thể tính được giới hạn. Ví dụ:
Giới hạn của hàm số f(x) = (x3 – 3x)/(x2 – 5x + 6) khi x tiến mang đến 3. Ta có:
limx→3 f(x) = limx→3 <(x – 3)x(x + 3)/(x – 2)(x – 3)>
Với x ≠ 3, ta có:
f(x) = (x – 3)x(x + 3)/(x – 2)(x – 3) = x(x + 3)/(x – 2)

Vì f(x) không xác định tại x = 3, ta có:
limx→3 f(x) = limx→3 x(x + 3)/(x – 2) = 18
Công thức 4: áp dụng khai triển Taylor
Trong một vài trường hợp, ta hoàn toàn có thể sử dụng triển khai Taylor nhằm tính số lượng giới hạn của hàm số. Khai triển Taylor cho phép chúng ta biểu diễn một hàm số ngẫu nhiên dưới dạng một chuỗi các đa thức trên một điểm xác định. Để tính số lượng giới hạn của hàm số, bọn họ chỉ cần tính giới hạn của những đa thức này. Ví dụ:
Giới hạn của hàm số f(x) = (sin x)/x lúc x tiến mang lại 0. Ta có:
f(x) = 1 – x2/3! + x4/5! – … = Σn=0 (-1)n x2n/(2n + 1)!

Để tính số lượng giới hạn của một hàm số, ta có thể sử dụng nhiều phương thức khác nhau, bao gồm định nghĩa, các công thức tính số lượng giới hạn và các định lý liên quan đến giới hạn.
Giới hạn vô cực, số lượng giới hạn ở vô cực
Nếu số lượng giới hạn của hàm số tiến đến vô cùng, bọn họ gọi kia là số lượng giới hạn vô rất (hoặc giới hạn ở vô cực). Khi tính giới hạn của một hàm số và cực hiếm của hàm số tiến mang đến vô cùng, họ sử dụng các phương pháp khác nhau tùy trực thuộc vào dạng của hàm số đó.
Nếu hàm số bị phân tách cho một hàm số khác mà lại giá trị của hàm số khác này tiến mang lại không hoặc vô cùng, bọn họ sử dụng cách thức chia để giải quyết và xử lý các việc này.
Giới hạn 1 bên
Trong ngôi trường hợp số lượng giới hạn của một hàm số ko tồn tại, hoặc giá bán trị giới hạn không thể xác minh được, chúng ta gọi kia là số lượng giới hạn một bên. Ví dụ, giới hạn của hàm số sin(x) ko tồn tại khi x tiến đến vô cùng.

Tìm số lượng giới hạn vô cùng của một dãy số
Tìm số lượng giới hạn vô thuộc của một dãy số bằng định nghĩa
Giới hạn của một hàng số là giá trị nhưng các phần tử của dãy số tiến cho đến khi số lượng bộ phận trong hàng số tiến mang đến vô cùng. Nếu số lượng giới hạn của hàng số tiến cho vô cùng, bọn họ gọi kia là số lượng giới hạn vô cùng.
Để tìm giới hạn vô cùng của một dãy số bởi định nghĩa, ta đề nghị kiểm tra xem hàng số có bị phân kỳ hay không. Nếu dãy số không bị phân kỳ và các giá trị của dãy số tiến cho vô cùng khi số lượng thành phần trong dãy số tiến mang đến vô cùng, thì giới hạn của dãy số là vô cùng.
Tìm số lượng giới hạn của một dày số bằng cách sử dụng định lý, nguyên tắc tìm số lượng giới hạn vô cực
Để tìm số lượng giới hạn của một hàng số, ta hoàn toàn có thể sử dụng các định lý với quy tắc liên quan đến giới hạn. Trong số những định lý phổ cập được thực hiện để chứng tỏ tính hóa học của giới hạn là định lý Vâyơstraxơ.
Chứng minh một hàng số có giới hạn:
Áp dụng định lý Vâyơstraxơ, nếu dãy số (un) tăng và bị chặn trên thì nó có giới hạn. Nếu hàng số (un) giảm và bị chặn dưới thì nó bao gồm giới hạn. Để chứng minh tính tăng với tính bị chặn, ta rất có thể thực hiện như sau:
CO3 + CO2 + H2O? tạo nên gì
Chứng minh một dãy số tăng và bị ngăn trên (dãy số tăng và bị ngăn dưới) vì số M ta thực hiện: Tính một vài ba số hạng đầu tiên của dãy và quan sát mối contact để dự đoán chiều tăng (chiều giảm) với số M.
Để tính số lượng giới hạn của hàng số, ta có thể sử dụng hai phương pháp sau:
Phương pháp 1: Đặt lim un = a. Từ lim u(n+1) = lim f(un) ta được một phương trình theo ẩn a. Giải phương trình tìm kiếm nghiệm a và số lượng giới hạn của hàng (un) là 1 trong trongcác nghiệm của phương trình đó.
Phương pháp 2: sử dụng quy tắc l’Hôpital. Nếu dãy số tất cả dạng không khẳng định (vô tỷ, vô cực trừ vô cực, không định dạng), ta rất có thể sử dụng luật lệ l’Hôpital để mang dãy số về dạng có thể tính được giới hạn. Sau đó, ta hoàn toàn có thể tính giới hạn bằng cách đặt giá trị đó bằng lim un.
Tóm lại, để tìm số lượng giới hạn vô cùng của một dãy số, bạn có thể sử dụng định nghĩa số lượng giới hạn vô thuộc hoặc các định lý với quy tắc liên quan đến giới hạn. Điều quan trọng là đề xuất kiểm tra xem dãy số gồm bị phân kỳ hay là không và áp dụng đúng các phương thức để tính giới hạn của hàng số.
Xem thêm: Một số câu giao tiếp tiếng nhật, những mẫu câu giao tiếp tiếng nhật hằng ngày
Bài tập vận dụng tìm giới hạn
Ví dụ 8: Tìm số lượng giới hạn saulim(x->0) (sin(2x) / x)
Để tính giới hạn của hàm số này, ta sử dụng cách thức chia tử và mẫu đến x để lấy biểu thức về dạng cơ bản:
sin(2x) / x = 2cos(2x) / 1
Khi đó, số lượng giới hạn của hàm số trở thành:
lim(x->0) (sin(2x) / x) = lim(x->0) (2cos(2x) / 1) = 2

Cao Đại Số
Cao Đại Số là 1 trong những tác giả với tương đối nhiều năm tay nghề trong nghành toán học. Hiện tại, ông đang làm người sáng tác viết bài cho trang web hueni.edu.vn với trình độ toán. Với việc đam mê và kiến thức và kỹ năng sâu rộng về toán học, Cao Đại Số vẫn đóng góp ít nhiều cho sự phát triển của ngành này. Thắng lợi của ông luôn luôn được đánh giá cao về tính thực tiễn và ứng dụng trong cuộc sống. Cửa hàng chúng tôi tin rằng, các nội dung bài viết của Cao Đại Số trên website hueni.edu.vn sẽ mang về nhiều quý hiếm cho cộng đồng học sinh, sinh viên cùng những tình nhân thích toán học.